Spectral Clustering Algorithms

We assume that our data consists of $n$ "points" $x_1,..., x_n$ which can be arbitrary objects. We measure their pairwise similarities $s_{ij} = s(x_i, x_j )$ by some similarity function which is symmetric and non-negative, and we denote the corresponding similarity matrix by $S = (s_{ij} )_{i,j=1...n}$.

Unnormalized spectral clustering
Input: Similarity matrix $S \in R^{n \times n}$, number $k$ of clusters to construct.

• Construct a similarity graph by one of the ways described in Section 2. Let $W$ be its weighted adjacency matrix.
• Compute the unnormalized Laplacian $L$.
• Compute the first $k$ eigenvectors $u_1,..., u_k$ of $L$.
• Let $U \in R^{n \times k}$ be the matrix containing the vectors $u_1,..., u_k$ as columns.
• For $i = 1,..., n$, let $y_i \in \Bbb R^k$ be the vector corresponding to the $i$-th row of $U$.
• Cluster the points $(y_i)_{i=1,...,n}$ in $\Bbb R^k$ with the $k$-means algorithm into clusters $C_1, . . . , C_k$.

Output: Clusters $A_1, ..., A_k$ with $A_i = \{j| y_j \in C_i\}$.

The normalized graph Laplacians

There are two different versions of normalized spectral clustering, depending which of the normalized graph Laplacians is used. 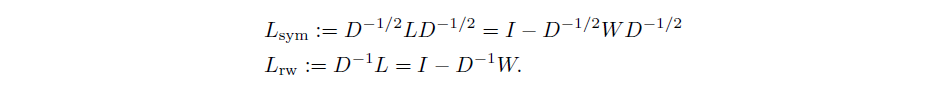We denote the first matrix by $L_{sym}$ as it is a symmetric matrix, and the second one by $L_{rw}$ as it is closely related to a random walk. In the following we summarize several properties of $L_{sym}$ and $L_{rw}$.

Normalized spectral clustering according to Shi and Malik (2000)
Input: Similarity matrix $S \in R^{n \times n}$, number $k$ of clusters to construct.

• Construct a similarity graph by one of the ways described in Section 2. Let $W$ be its weighted adjacency matrix.
• Compute the unnormalized Laplacian $L$.
• Compute the first $k$ generalized eigenvectors $u_1,..., u_k$ of the generalized eigenproblem $Lu = \lambda Du$.
• Let $U \in R^{n \times k}$ be the matrix containing the vectors $u_1,..., u_k$ as columns.
• For $i = 1,..., n$, let $y_i \in \Bbb R^k$ be the vector corresponding to the $i$-th row of $U$.
• Cluster the points $(y_i)_{i=1,...,n}$ in $\Bbb R^k$ with the $k$-means algorithm into clusters $C_1, . . . , C_k$.

Output: Clusters $A_1, ..., A_k$ with $A_i = \{j| y_j \in C_i\}$.

Note that this algorithm uses the generalized eigenvectors of $L$, which according to Proposition 3 correspond to the eigenvectors of the matrix $L_{rw}$. So in fact, the algorithm works with eigenvectors of the normalized Laplacian $L_rw$, and hence is called normalized spectral clustering. The next algorithm also uses a normalized Laplacian, but this time the matrix $L_sym$ instead of $L_rw$. As we will see, this algorithm needs to introduce an additional row normalization step which is not needed in the other algorithms.

Normalized spectral clustering according to Shi and Malik (2000)
Input: Similarity matrix $S \in R^{n \times n}$, number $k$ of clusters to construct.

• Construct a similarity graph by one of the ways described in Section 2. Let $W$ be its weighted adjacency matrix.
• Compute the unnormalized Laplacian $L$.
• Compute the first $k$ generalized eigenvectors $u_1,..., u_k$ of the generalized eigenproblem $Lu = \lambda Du$.
• Let $U \in R^{n \times k}$ be the matrix containing the vectors $u_1,..., u_k$ as columns.
• Form the matrix $T \in \Bbb R^{n\times n}$f rom $U$ by normalizing the rows to norm 1,that is set $t_{ij}=u_{ij}/(\sum_k u_{ik}^2)^{1/2}$.
• For $i = 1,..., n$, let $y_i \in \Bbb R^k$ be the vector corresponding to the $i$-th row of $U$.
• Cluster the points $(y_i)_{i=1,...,n}$ in $\Bbb R^k$ with the $k$-means algorithm into clusters $C_1, . . . , C_k$.

Output: Clusters $A_1, ..., A_k$ with $A_i = \{j| y_j \in C_i\}$.

In all three algorithms, the main trick is to change the representation of the abstract data points $x_i$ to points $y_i \in \Bbb R^k$. It is due to the properties of the graph Laplacians that this change of representation is useful. We will see in the next sections that this change of representation enhances the cluster-properties in the data, so that clusters can be trivially detected in the new representation. In particular, the simple k-means clustering algorithm has no difficulties to detect the clusters in this new representation.